what is two to the power of zero
The " Zilch Power Rule" Explained
Exponents seem pretty straightforward, right? Raise a number to the power of one means you lot accept one of that number, raise to the power of 2 means yous have ii of the number multiplied together, ability 3 means three of the number multiplied together and so on.
But what about the zippo power? Why is any not-zero number raised to the ability of nada equal i? And what happens when we raise zero to the cipher power? Is it still 1?
Watch the video or read below to detect out!
Warm-Upward Example
Allow'due south begin past examining division of values with exponents.
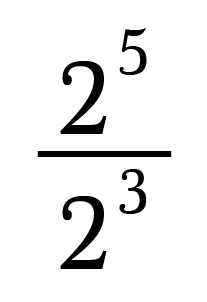
Think exponents represent repeated multiplication. Then we tin rewrite the above expression equally:

Since 2/2 = 1, abolish out 3 sets of two/ii. This leaves 2 • 2, or 2 squared.
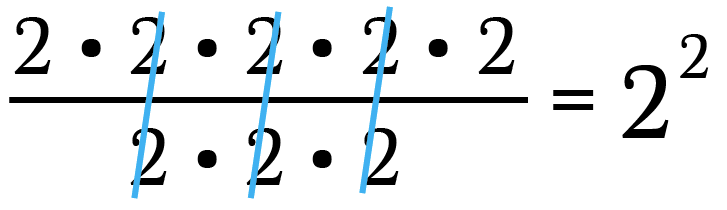
Of course we tin can take a shortcut and subtract the number of 2's on lesser from the number of 2's on top. Since these quantities are represented by their respective exponents, all nosotros need to do is write the common base with the difference in exponent values as the power.

If we generalize this rule, we have the post-obit where north represents a non-zero real number and x and y are also real numbers.
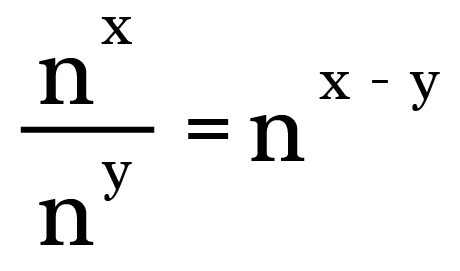
Exploring the Zero Power
From here it is easy to derive the explanation for why any non-zero number raised to the zero power equals 1. Again, allow'southward look at a concrete instance.
Nosotros know that any not-zilch number divided past itself equals 1. So I can write the post-obit:
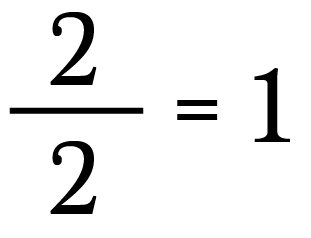
This is the same as writing:
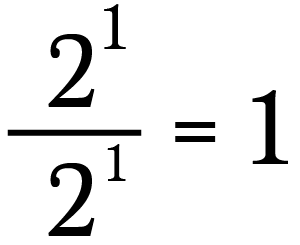
At present I'll utilise the exponent rule from above to rewrite the left hand side of this equation.
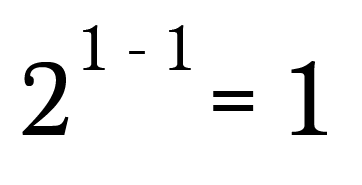
Of form, this is equivalent to:
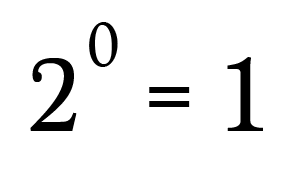
We tin can use the same process as in this case, along with the generalized rule above, to show that any non-zero existent number raised to the nothing power must result in ane.
What Near Zero to the Aught Power?
This is where things get catchy. The in a higher place method breaks because, of grade, dividing by nothing is a no-no. Permit's examine why.
We'll begin with looking at a common divide by nothing Mistake .
How about 2÷0? Let's await at why we can't practice this.

Division is really just a form of multiplication, and so what happens if I rewrite the above equation as:
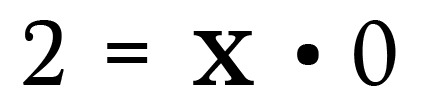
What value could possible satisfy this equation for ten?
At that place is no value! Any number times nil results in null, it can never equal 2. Therefore, we say sectionalisation by zero is undefined. There is no possible solution.
Now let's expect at 0÷0.
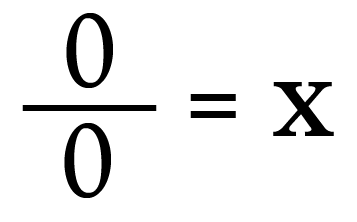
Over again, rewrite it equally a multiplication problem.
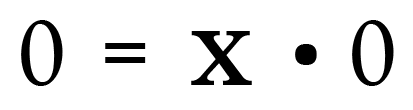
Hither nosotros encounter a very different state of affairs. The solution for x could exist Any real number! There is no way to decide what 10 is. Hence, 0/0 is considered indeterminate*, not undefined.
If we try to employ the above method with zero equally the base to determine what nil to the goose egg ability would be, we come to halt immediately and cannot continue because nosotros know that 0÷0 ≠ 1, but is indeterminate.
Then what does zero to the aught ability equal?
This is highly debated. Some believe information technology should be defined equally 1 while others recall it is 0, and some believe it is undefined. There are good mathematical arguments for each, and peradventure it is nigh correctly considered indeterminate.
Despite this, the mathematical community is in favor of defining zero to the zero power every bit 1, at least for nigh purposes.
Perchance a helpful definition of exponents for the amateur mathematician is as follows:
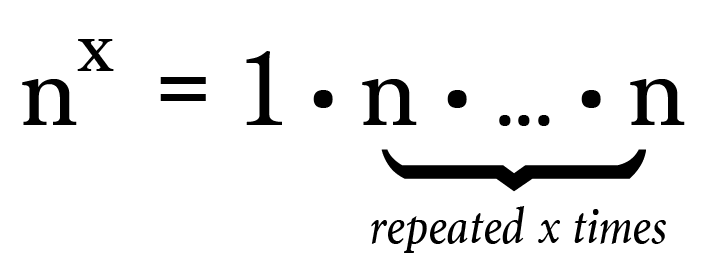
By including the "1" in the definition, we can conclude that any number (including nada) repeated zero times results in 1.
*Calculus Note:
The notion of indeterminate forms is commonplace in Calculus. A simple example of why 0/0 is indeterminate can be found past examining some basic limits.
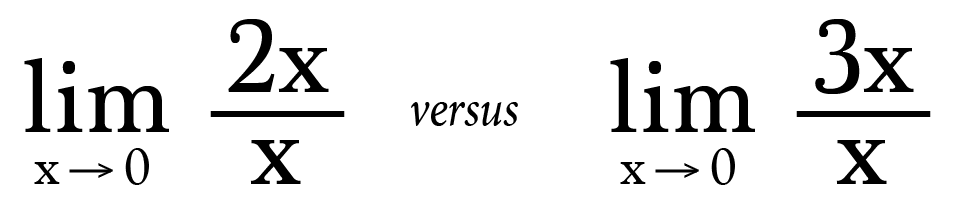

These limits cannot be straight evaluated since they are indeterminate forms. Instead we must utilize L'hopital's rule, taking the derivative of the numerator and denominator separately, to find the solutions are 2 and 3 respectively.
When dealing with an equation that results in an indeterminate form of zero to the zero power while practicing Calculus, brand certain to implement techniques for indeterminates, such as L'hopital'south dominion, to correctly evaluate the limit.
❤ STAY Continued ❤
Stay upwardly-to-date with everything Math Hacks is up to!
Instagram | Facebook | Twitter
Next Lesson: Common Misconception Well-nigh Probability
Related Reads
Source: https://medium.com/i-math/the-zero-power-rule-explained-449b4bd6934d
0 Response to "what is two to the power of zero"
Post a Comment